Có thể nói, toán là một trong những môn học được cho là nỗi ám ảnh của rất nhiều học sinh. Bởi không chỉ có nhiều định nghĩa, ký hiệu mà học sinh phải ghi nhớ. Bên cạnh đó còn là hàng ngàn các công thức toán với những dạng bài toán khác nhau. Bài viết ngày hôm nay sẽ giúp các bạn học sinh phần nào nắm rõ được một trong những công thức thường gặp trong chương trình giáo dục chính là công thức tính diện tích hình chóp tam giác đều. Cùng theo dõi bài viết để hiểu rõ và cụ thể hơn về công thức này nhé!

Môn toán – môn học khó nhằn đối với nhiều học sinh, sinh viên

Khái niệm: Thế nào là hình chóp tam giác đều?

Định nghĩa hình chóp tam giác đều:

Hình chóp tam giác đều là hình gì?

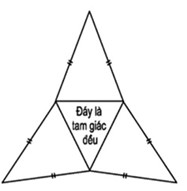
Nếu như hình chóp có đáy là một tam giác đều và phải thỏa điều kiện các mặt bên (mặt cạnh bên) đều bằng nhau thì chính ta gọi đó là hình chóp tam giác đều.

Bên cạnh đó, nếu như một hình chóp mà hình chiếu của đỉnh hình chóp đó trùng với tâm của tam giác đều thuộc hình chóp đó thì gọi là hình chóp tam giác đều.

Hình ảnh minh họa: hinh chóp tam giác đều

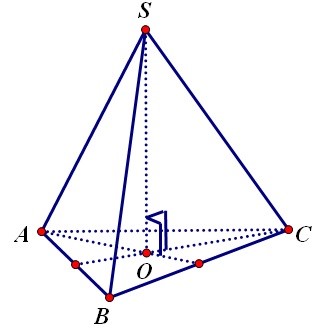
Các tính chất của 1 hình chóp tam giác đều:

Hình chóp tam giác đều luôn có đáy là một hình tam giác đều

Hình chóp tam giác đều luôn có các tính chất sau đây:

• Đáy của hình chóp đó luôn luôn là một tam giác đều,
• Các cạnh bên của hình chóp tam giác đều thì luôn bằng nhau,
• Các mặt bên của hình chóp tam giác đều luôn là tam giác đều (có thể là tam giác đều, tức không nhất thiết các mặt bên của hình chóp tam giác đều đều là tam giác đều),
• Chân đường cao (hình chiếu của đỉnh hình chóp tam giác đều) luôn trùng với trọng tâm của đáy tam giác (tâm đáy của hình chóp tam giác đều),
• Góc được tạo bởi mặt đáy và mặt bên thì đều bằng nhau.

Phân biệt giữa tứ diện đều và hình chóp tam giác đều:

Tứ diện đều chính là một trường hợp đặt biệt của hình chóp tam giác đều nghĩa là không chỉ mặt đáy là hình tam giác đều mà các mặt bên của tứ diện đều đều là hình tam giác đều.

Nghĩa là tứ diện đều thì chính là hình chóp tam giác đều nhưng không phải hình chóp tam giác đều nào thì cũng là tứ diện đều. Vì sao?

Vì như đã đề cập ở tính chát của hình chóp tam giác đều. Các mặt bên luôn là tam giác cân, không nhất thiết phải là tam giác đều. Nhưng nếu muốn là một tứ diện đều thì các mặt bên của hình chóp tam giác đều thì đều phải là tam giác đều. Vì thế mà không phải hình chóp tam giác đều nào cũng là tứ diện đều.

Tham khảo thêm :

• Công thức tính diện tích mặt cầu ngoại tiếp hình chóp chuẩn
• Công thức tính thể tích hình hộp chữ nhật kèm ví dụ hay
• Tổng hợp công thức tính diện tích và chu vi hình chữ nhật

Hình ảnh ví dụ và cách vẽ hình chóp tam giác đều:

Hình ảnh ví dụ về hình chóp tam giác đều:

Hình ảnh ví dụ về hình chóp tam giác đều

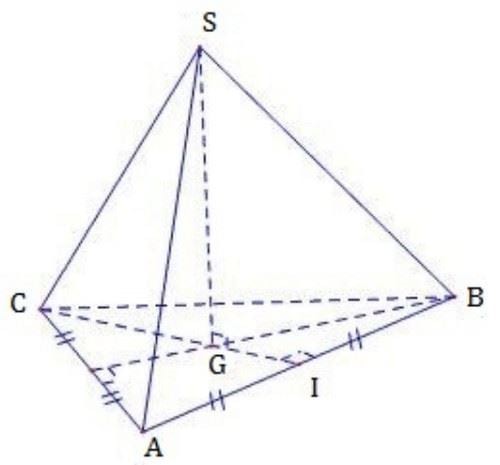
Phía trên là hình ảnh về hình chóp tam giác đều S.ABC, có S là đỉnh là của hình chóp và G là tâm đáy của hình chóp tam giác đều.

Cách vẽ hình chóp tam giác đều :

Muốn giải một bài toán hình bất kì nào đó thì việc đầu tiên chúng ta cần làm một cách thật chính xác và kỹ lưỡng chính là vẽ chính xác hình mà đề bài đưa ra.

Và các bài toán về hình chóp tam giác đều cũng vậy, bên cạnh đó, vẽ ình cũng nằm trong danh mục được tính điểm khi đi thi vì vậy các bạn cần lưu ý vấn đề này để tránh bị mất điểm.

Muốn vẽ được hình chóp tam giác đều chính xác và dễ dàng thì các bạn cần thực hiện 3 bước theo thứ tự sau đây:

• Bước 1: vẽ một hình tam giác đều ABC (nhưng không cần nhất thiết ba cạnh phải bằng nhau, có thể vẽ một hình tam giác bình thường vì trong hình học không gian là hình 3D vì thế nhìn theo các góc độ khác nhau thì độ dài các cạnh sẽ có sự thay đổi),
• Bước 2: Lần lược, vẽ 2 đường trung tuyến AI và CF cắt nhau tại điểm O, và điểm O này cũng chính là chân đường cao của đỉnh hình chóp trùng với tâm đáy (tâm của tam giác đều ABC),
• Bước 3: Từ O, ta dựng 1 đường thẳng đứng, từ đó ta có được đỉnh S của hình chóp. Cuối cùng, lần lượt nối đỉnh S của hình chóp với 3 đỉnh A, B, C của đáy hình chóp (tức tam giác đều ABC).

→ Ta hoàn thành hình vẽ và thu được một hình chóp tam giác đều S.ABC, với SH là đường cao và SA = SB = SC.

Công thức tính diện tích xung quang của hình chóp tam giác đều :

Phát biểu công thức tính diện tích xung quanh của hình chóp tam giác đều: “Muốn tính diện tích xung quanh của một hình chóp tam giác đều, ta lấy độ dài trung đoạn của hình chóp tam giác đều nhân với nữa chu vi đáy của hình chóp đó.

Hay phải biểu một cách xúc tích hơn thì diện tích xung quanh của hình chóp tam giác đều chính là tích của nửa chu vi đáy với trung đoạn của hình chóp đó.

Ta có công thức tổng quát tính diện tích xung quanh của hình chóp tam giác đều:

S xung quanh = p *  d

Trong đó:

• S xung quanh: chính là diện tích xung quanh
• p: là nửa chu vi đáy hình chóp tam giác đều 
• d: là độ dà trung đoạn của hình chóp

Ví dụ:

Cho một hình chóp tam giác đều có chiều dài cạnh đáy là 4 cm và trung đoạn của hình chóp tam giác đều là 2 cm. Hãy tìm diện tích xung quanh của hình chóp tam giác đều đó?

Lời giải:

Đầu tiên, theo công thức tính diện tích xung quanh của hình chóp tam giác đều vừa nêu trên, ta cần xác định được nửa chu vi của đáy hình chóp tam giác đều là bao nhiêu.

Vì là hình chóp tam giác đều nên đáy của hình chóp là một tam giác đều. Từ đó, ta áp dụng công thức tính nữa chu vi hình tam giác đều.

Nửa chu vi đáy của hình chóp tam giác đều là: 

p = (3 x 4) ÷ 2 = 6 (cm)

→ Diện tích xung quanh của hình chóp tam giác đều là:

S xung quanh = p * d

=> S xung quanh = 6 2 = 18 (cm2)

→ Kết luận: diện tích xung quanh của hình chóp tam giác đều là 16 cm2.

Công thức tính diện tích toàn phần của hình chóp tam giác đều :

Phát biểu công thức tính diện tích hình chóp tam giác đều: Diện tích toàn phần của hình chóp tam giác đều chính tổng của diện tích xung quang với diện tích mặt đấy của hình chóp tam giác đều đó.

Công thức tổng quát tính diện tích toàn phần của hình chóp tam giác đều là: 

S toàn phần = S xung quanh + S đáy

Trong đó: 

• S toàn phần : là diện tích toàn phần của hình chóp
• S xung quanh : là diện tích xung quanh của hình chóp
• S đáy : là diện tích đáy của hình chóp

Ví dụ:

Cho một hình chóp tam giác đều có đội dài cạnh là 5cm, chiều cao của mặt đáy hình chóp là 4 cm và đường cao trung đoán của hình chóp là 2 cm. Hãy xác định diện tích toàn phần của hình chóp tam giác đều đó?

Lời giải:

Ta có, nửa chu vi đáy của hình chóp tam giác đều:

p = (5 x 3) ÷ 2 = 7,5 (cm) 

Diện tích xung quanh của hình chóp tam giác đều là:

S xung quanh = 7,5 2=15 (cm2)

Diện tích đáy của hình chóp tam giác đều là:

S đáy = (4 5) 2 = 10(cm2)

Theo công thức tính diện tích toàn phần của hình chóp tam giác đều, ta có:

S toàn phần = S xung quanh + S đáy

S toàn phần = 15 + 10 = 25 (cm2)

→ Kết luận: diện tích toàn phần của hình chóp tam giác đều là 25 (cm2)