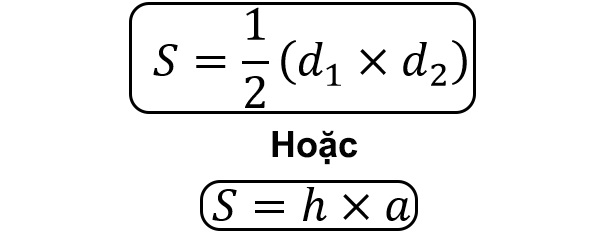Công thức tính diện tích hình thoi và chu vi hình thoi 2024

Từ cấp 2 chúng ta đã được tiếp xúc với hình học không gian hoặc các phép tính liên quan đến toán học. Bài viết dưới đây sẽ ôn tập lại kiến thức về hình thoi và các công thức tính diện tích hình thoi và chu vi hình thoi . Mời các bạn hãy cùng theo dõi nhé.

Hình thoi là gì?

Hình thoi là hình tứ giác có 4 cạnh bằng nhau hoặc hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau

Nhận biết hình thoi

Ngoài ra hình thoi còn có 2 tên gọi khác để bổ sung thay thế cho nhau là Lozenge và kim cương. Muốn tìm hiểu các công thức diện tích hình thoi hay thể tích hình thoi thì bước đầu tiên phải xác định được hình thoi là gì.

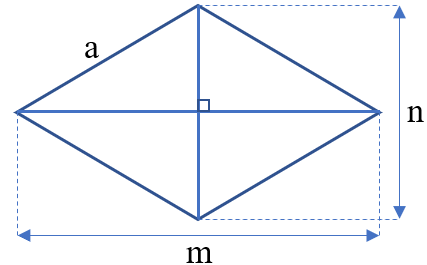
Hình minh họa hình thoi

Trong hình học không gian, hình thoi được cho là hình tứ giác có 4 cạnh bằng nhau. Và chúng còn tồn tại ở nhiều dạng hình học khác nhau như bình hành sẽ có 2 cạnh liền kề, có các số đo giống nhau hay hình bình hành có 2 đường chéo mà chúng vuông góc với nhau.

Tính chất cơ bản của hình thoi như sau:

Hai đường chéo của hình thoi có vuông góc với nhau và chúng cắt nhau ở mỗi trung điểm của các đoạn đường.
Hai đường chéo của hình thoi là các đường phân giác hình thoi của các góc trong hình.
Hình thoi bao gồm các tính chất, đặc điểm của hình bình hành.

Tham khảo thêm các công thức toán học khác :

Đặc điểm nhận biết dấu hiệu của hình thoi

Dấu hiệu của hình thoi được nhận biết từ hình tứ giác đặc biệt:

Hình tứ giác mà có 4 cạnh bằng nhau thì là hình thoi.
Hình tứ giác mà có 2 đường chéo làm thành đường trung trực thì là hình thoi.
Hình tứ giác mà có 2 đường chéo làm thành đường phân giác cho cả 4 góc thì là hình thoi.

Công thức diện tích hình thoi cũng hình thành từ các đường chéo, các trung điểm trong trong hình tứ giác.

Dấu hiệu nhận biết hình thoi từ hình bình hành:

Hình thoi là một dạng hình học theo kiểu đặc biệt của hình bình hành bởi vì nó có tất cả các yếu tố của hình bình hành:

Hình bình hành mà có 2 cạnh bên bằng nhau thì la hình thoi.
Hình bình hành mà có 2 đường chéo tạo thành góc vuông với nhau thì là hình thoi.
Hình bình hành mà có 1 đường chéo tạo thành đường phân giác của 1 góc thì là hình bình hành.

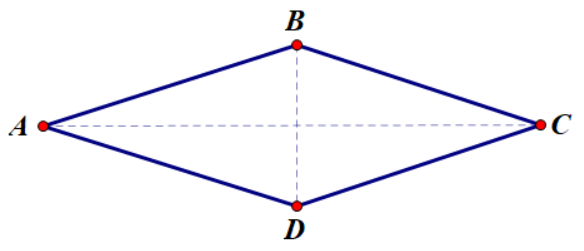
Hình thoi ABCD được cắt bởi hai đường chéo

Sau khi phân biệt được hình thoi là loại hình gì thì tiếp theo chúng ta sẽ cùng nhau tìm hiểu về các công thức diện tích hình thoi và tính thể tích hình thoi. Hy vọng những phép tính dưới đây sẽ giúp ích cho các bạn.

Công thức diện tích hình thoi chuẩn SGK

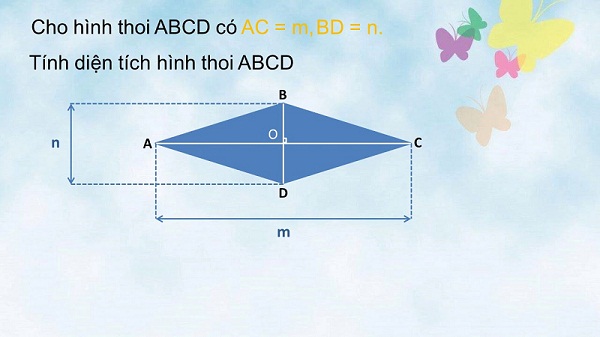
Công thức diện tích của hình thoi được xác định bằng một nửa tích hai đường chéo hay bằng tích của chiều cao tương ứng với cạnh đáy hình thoi.

Dùng đường chéo hình thoi để ra công thức tính diện tích hình thoi :

Shình thoi = (d1 x d2)1/2

Từ công thức này suy ra chúng ta phải tìm độ dài của mỗi đường chéo hình thoi. Đường chéo là đường nối với các đỉnh đối diện hình thoi, hai đường chéo trong hình thoi sẽ vuông góc với nhau tại giao điểm đặt ở trong hình.

Bước tiếp theo nhân hai đường chéo lại với nhau, nếu như có độ dài thì tìm độ dài hai đường chéo theo cách trên, nếu đã cho sẵn thì lấy độ dài có sẵn nhân lại.

Cuối cùng tổng hợp tất cả số đo của hai đường chéo nhân cho nhau rồi đem chia cho 2 và hoàn thành công thức diện tích hình thoi.

Chú thích:

S là kí hiệu cho diện tích hình thoi
d1, d2 sẽ lần lượt thể hiện kích thước cho hai đường chéo trong hình thoi

Dùng độ dài của cạnh đáy hình thoi và chiều cao để ra diện tích hình

Shình thoi = a x h

Công thức diện tích hình thoi từ việc tìm chiều cao và độ dài của cạnh đáy hình thoi. Khi đã biết độ dài của đáy, chiều cao của hình thì ta cứ áp dụng công thức để tính toán cho ra kết quả chính xác nhất.

Công thức diện tích hình thoi

Chú thích:

S là kí hiệu cho diện tích hình thoi
h là chiều cao được xác định trong hình thoi
a là độ dài tương ứng với cạnh đáy của hinh thoi

Dùng hệ thức lượng của hình tam giác để tính diện tích:

Lấy độ dài cạnh bình phương lên lấy bắt kì cạnh nào cũng được vì hình thoi có độ dài 4 cạnh bằng nhau. Nhân với giá trị sin, cos, tan của lượng giác cho ra cách tính diện tích hình thoi theo hệ thức lượng giác.

Công thức chu vi hình thoi theo chuẩn SGK

Cách tính chu vi hình thoi bằng tổng độ dài các cạnh cộng lại với nhau hoặc độ dài một cạnh nhân với 4. Cụ thể công thức tính chu vi như sau :

P = a x 4

– Trong đó:

+ P: Chu vi hình thoi.

+ a: Độ dài một cạnh bất kỳ của hình thoi .

Khi chúng ta đã nắm vững chắc công thức tính chu vi này rồi chúng ta hoàn toàn có thể thực hiện nhiều cách để tính chu vi hình thoi nhé .

Các ví dụ thực tế từ cách tính chu vi hình thoi và diện tích của hình thoi:

Tổng hợp các bài luyện tập liên quan đến hình thoi như tính diện tích, chu vi cho mọi người có thể dễ dàng thực hành ngay say khi có công thức .

Ví dụ 1: Bài tập cho hình thoi BCDE có cạnh BE = 6cm. Có góc EBC = 30 độ. Áp dụng công thức diện tích hình thoi vào bài toán để tính hình thoi BCDE có diện tích là bao nhiêu?

Bài giải :

Cho hình thoi BCDE có các cạnh là tam giác nên tạo thành hình tam giác cân trong hình. Đặt F là trung điểm cho 2 đường chéo của hình thoi, BF vuông góc với CE, góc FBC = 15 độ ( bằng một nửa góc lớn EBC ). Cho nên BF = B. cos FBC = 6cm. Cos của 15 độ bằng 3.84m.

Đầu tiên xét tam giác vuông của BCF, theo định lý toán học Pytago. Suy ra ta có:

CF2 = BC2 – BF2 = 1.25m. Nên BI = 1.1m.
BD = 2 x BF = 7.68m
BE = 2 x CF = 2.2m

Áp dụng công thức diện tích hình thoi

BCDE = ½ x BD x CE = 8.45 (m2)

Ví dụ 2 : Bài tập toán cho hình thoi BCDE có cạnh BC = 6cm. Có số đo đường chéo BD= 8cm. Áp dụng công thức diện tích hình thoi vào bài toán để tính hình thoi BCDE có diện tích là bao nhiêu?

Bài giải:

F được tính là giao điểm của BC và BD của hình thoi BCDE. Suy ra ta có BF = FD = 4cm.

Xét tam giác vuông BCF trong hình thoi BCDE:

CF2 = BC2 – BF2
Thay BF = 4cm, BC = 6cm, ta sẽ có được góc CF = 3cm
Mà CE = 2 x CF = 2 x 3 = 6cm

Hình thoi có 2 đường chéo lần lượt là d1= 6cm, d2 = 8cm

Áp dụng công BCDE:

Shình thoi = ( CE x BD ) : 2 = 24cm2

Ví dụ 3 : Cho một ví dụ đơn giản hơn về công thức diện tích hình thoi đơn giản nhất theo độ của đường chéo được cho sẵn. Đề bài cho 2 đường chéo lần lượt là d1 = 5cm, d2 = 12cm. Tính diện tích hình thoi?

Giải bài tập :

Shình thoi = ½ ( d2 x d1 ) = ½ ( 5 x 12 ) = 30cm2

Các lưu ý khi áp dụng công thức tính diện tích của hình thoi

Khi sử dụng công thức diện tích hình thoi chúng ta cần biết những điều sau đây để tránh gây nhầm lẫn và làm sai khi tính toán:

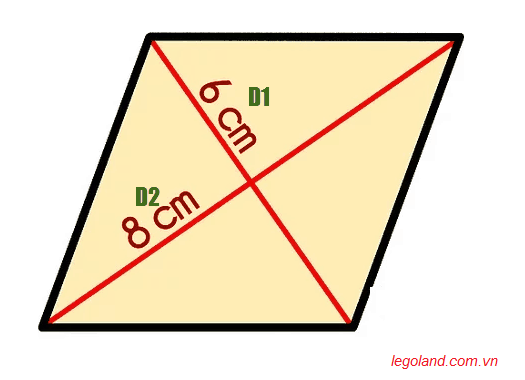
Cần xác định rõ rồi mới áp dụng công thức tính diện tích hình thoi

Hình thoi không giống với hình vuông nhưng lại khá giống hình bình hành, có rất nhiều bạn nhầm lẫn nếu vẽ các đường chéo trong hình thì sẽ thành hình thoi. Nhưng định lý này đã sai vì hình vuông khi vẽ đường chéo chỉ có thể thành hình tam giác cân, tam giác vuông,… Chứ không thể ra hình thoi. Vì vậy không nên áp dụng công thứcdiện tích hình thoi vào hình vuông.
Khi áp dụng công thức diện tích hình thoi chu vi hình thoi thì nên để ý các đơn vị của diện tích hình thoi là số đo đã được tính cộng với vuông như mét vuông (m2), căng ti mét vuông (cm2),…
Trước khi làm bài nên đọc kĩ đề, đề kêu xác định tính toán phần nào thì tính toán phần đó. Đặc biệt lưu ý nếu như các số đo trong đề chưa quy đổi theo đúng đơn vị chuẩn thì phải lập tức chuyển qua số đo đúng đơn vị.

Hy vọng bài viết về công thức tính diện tích hình thoi và thể tích hình thoi sẽ mang đến cho bạn nhiều kiến thức bổ ích. Việc học chưa bào giờ là kết thúc, học nữa học mãi học tới khi chúng ta không thể học. Với những công thức trên các bạn có thể áp dụng vào lĩnh vực đời sống, lĩnh vực học tập thậm chí bổ sung nhiều kĩ năng trong công việc.