Dưới đây sẽ là bài viết tổng hợp các kiến thức về vòng tròn lượng giác và các bài tập liên quan đến vòng tròn lượng giác. Đừng bỏ lỡ bài viết này nhé, nếu như bỏ lỡ thì bạn sẽ bỏ qua một kho tàng kiến thức bổ ích đấy.
Khái niệm về vòng tròn lượng giác là gì?
Theo như lý thuyết thì một dao động điều hòa sẽ có phương trình của x = Acos(ωt + φ), chúng có thể biểu diễn bằng một vòng tròn lượng giác. Dựa theo hình học để biểu diễn trên đường tròn, kết hợp lại với công thức tính lượng giác ta vẫn có thể suy ra các đại lượng vật lý đang tìm kiếm như biên độ A hay li độ x và thời gian t,… tùy theo dữ kiện đã cho trước và câu hỏi được đặt ra.
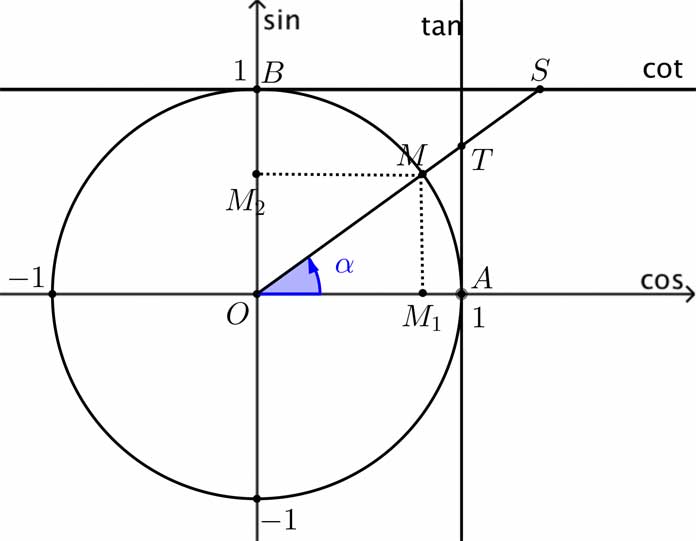
Vòng tròn lượng giác là một đường tròn của đơn vị tâm O và bán kính 1
Vòng tròn lượng giác là một đường tròn của đơn vị tâm O và bán kính 1, được định hướng bởi quy ước chiều dương cũng là chiều ngược với chiều kim đồng hồ và trên đó điểm A, chính là điểm gốc.
Điểm P\left( x,y \right) nằm trên vòng tròn lượng giác làm sao cho một điểm C có bất kì nhưng vẫn nằm trên đường tròn, suy ra ta đều có \left( OA,OC \right)=\alpha thì được gọi là điểm nằm trên đường tròn lượng giác và được biểu diễn bằng cung lượng giác có số đo \alpha.
- Trục Ox có tên gọi là trục giá trị cos.
- Trục Oy có tên gọi là trục giá trị sin.
- Trục tan có gốc tương xứng chính là điểm mà cũng vuông góc chung với trục cos lẫn luôn trục cotan có gốc, hay được gọi là điểm vuông góc với trục sin.
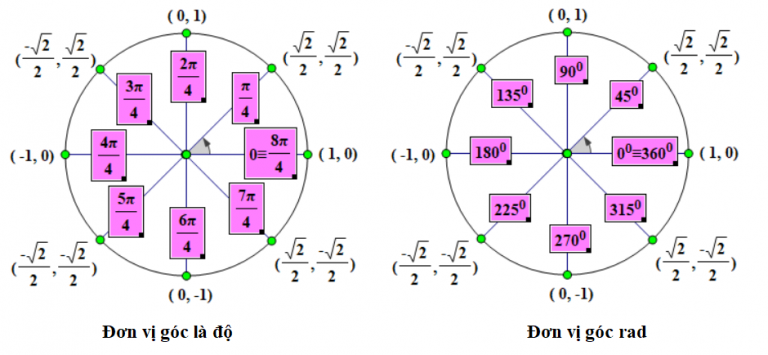
Dấu hiệu và giá trị của lượng giác trong vòng tròn lượng giác là gì?
Dấu của các giá trị lượng giác trong vòng trong lượng giác là gì?
Dưới đây sẽ là các dấu hiệu nhận biết của lượng giác trong vòng tròn lượng giác:
| Góc phần tư số | I | II | III | IV |
| Giá trị lượng giác | ||||
| sin x | + | + | – | – |
| cos x | + | – | – | + |
| tan x | + | – | + | – |
| cot x | + | – | + | – |
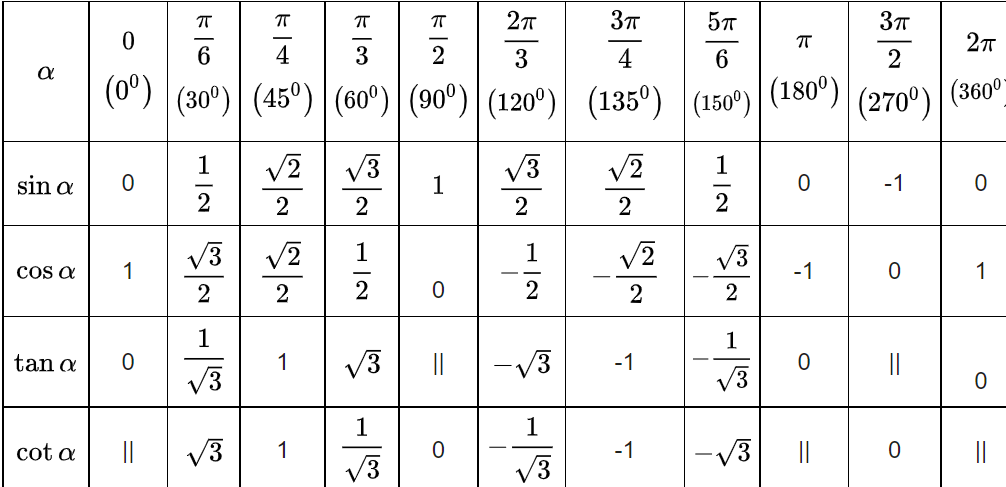
Bảng giá trị lượng giác từ 0 độ đến 180 độ:
Bảng giá trị lượng giác trong vòng tròn lượng giác từ 0 độ đến 180 độ:
Bảng giá trị lượng giác
Các công thức để tính toán trong vòng tròn lượng giác là gì?
Muốn sử dụng được vòng tròn lượng giác để giúp giải những bài tập vật lý và toán thì các em cần phải ghi nhớ được rằng tất cả các công thức liên quan đến vòng tròn lượng giác một cách chính xác và đủ đầy nhất bao gồm:
Công thức cơ bản của vòng tròn lượng giác:
- Sin2x + cos2x =1
- Tanx = sinx : cosx
- Cotx = cosx : sinx
- Tanx.cotx = 1
- 1+tan2x = 1 : cos2x
- 1 + cot2x = 1 : sin2x
Công thức cộng của vòng tròn lượng giác bao gồm:
- Cos (a+b) = cosa x cosb – sina x sinb
- Cos (a-b) = cosa x cosb + sina x sinb
- Sin (a+b) = sina x cosb + sinb x cosa
- tan (a+b) = (tana + tanb) : (1 – tana.tanb)
- tan (a-b) = (tana – tanb) : (1 + tana.tanb)
Công thức nhân đôi và hạ bậc của vòng tròn lượng giác:
Khi học về những kiến thức của vòng tròn lượng giác tại năm lớp 11, thì công thức nhân đôi cũng như công thức hạ bậc là kiến thức chiếm tỉ phần vô cùng quan trọng. Nếu các bạn không thể ghi nhớ hết 2 phần kiến thức này thì sẽ không bao giờ giải được bất kì 1 bài toán nào về những kiến thức liên quan đến lượng giác cả.
Hãy ghi nhớ công thức vòng tròn lượng giác
Cũng chính vì vậy, khi học bài hay nghe giảng về vòng tròn của lượng giác thì hãy thường xuyên ghi chép và phải thực hành sử dụng để ghi nhớ các công thức sau đây:
- Sin2a = 2sina x cosa, tan 2a = 2tana : (1 – tan²a)
- Cos2a = 2cos²a – 1 = 1 – 2sin²a = cos²a – sin²a
- Sin²a = (1-cos2a) : 2, cos²a = (1+ cos2a) : 2
- Cos3a = 4cos³a – 3cosa ⇒ cos³a = (3cosa + cos3a) : 4
- Sin3a = 3sina – 4sin³a ⇒ sin³a = (3sina -sin3a) : 4
Công thức biến đổi từ tổng thành tích của vòng tròn trong lượng giác:
- Cosa + cosb = 2cos (a+b) : 2 x cos (a-b) : 2
- Cosa – cosb = -2sin(a+b)2 x sin (a-b) : 2.
- Sina+sinb = 2sin(a+b)/2 x cos (a-b) : 2
Công thức biến đổi từ tích thành tổng vòng tròn trong lượng giác:
- Cosa x cosb = 1/2 [cos (a-b) +cos (a+b)]
- Sina x sinb = 1/2 [cos(a-b)- cos(a+b)]
- Sina x cosb = 1/2 [ sin (a-b) + sin (a+b)]
Ứng dụng công thức vòng tròn lượng giác vào cách giải bài tập vật lý như thế nào?
Những bạn nào đang trong quá trình học lớp 11 và thường hay sử dụng vòng tròn lượng giác để có thể giải nhanh những bài tập thì chắc chắn bạn sẽ thấy được sự tiện ích và lợi hại của chúng.
Như các bạn cũng đã biết thì một câu hỏi trong vật lý nếu như chỉ đọc sơ qua thì sẽ thấy vấn đề này nó quá phức tạp nhưng thực tế khi biết sử dụng đúng những công thức tính toán thì ngược lại xử lý cực nhanh gọn ví dụ như dùng vòng tròn lượng giác.
Có thể ứng dụng để giải bài tập vật lý
Các bạn có thể ứng dụng vòng tròn lượng giác vào các dạng bài này để giải như sau đây:
- Dạng bài liên quan về dao động điều hòa
- Giải các bài toán liên quan về giới gian
- Hay tính quãng đường đi của vật
Trên đây là những dạng bài và kiến thức có trong bài giảng về vòng tròn trong lượng giác mà các bạn học sinh cần phải luôn đặc biệt ghi nhớ, bởi vì chúng có thể giúp ích cho việc học tập của ta trở nên nhanh chóng đồng thời dễ dàng, hiệu quả hơn.
Các bài tập áp dụng công thức vòng tròn lượng giác trong vật lý:
Một số bài tập vật lý có thể áp dụng vòng tròn lượng giác trong vật lý như sau:
Bài tập 1: Một chất điểm mà dao động điều hòa theo dạng của phương trình sau đây: x = 4 x cos(πt + π/3), với giá trị x được tính bằng cm còn t thì tính bằng giây. Thời điểm mà vận tốc v của chất điểm đó đạt được giá trị -2π cm/s đến lần thứ 7 là:
- 6,5 s. B. 4,5 s. C. 2,5 s. D. 6,75 s.
Bài giải:
Xác định được thời điểm, suy ra dùng đường tròn đa điểm để ứng với 1 trục x,v như sau : A = 4cm và vmax = 4π cm/s.
Thời điểm ban đầu của một ly độ sẽ là Mox. Do vận tốc đi nhanh quá pha với π/2 ứng tại li độ vào thời điểm ban đầu của chính vận tốc là Mox, còn đứng trước Mox là một góc π/2.
Vận tốc -2π cm/s có thể tương ứng với M1 lẫn M2 trên cùng một đường tròn.
N = 7 thì sẽ bằng 3.2 + 1 lần,
Bài tập 2: một mẫu vật nhỏ có dao động điều hòa nằm trên trục Ox, có biên độ bằng 2 cm và có cả tần số bằng 2 Hz. Chúng ta lấy gần đúng với π2 = 10. Trong khoảng thời gian ngắn nhất ta phải tính từ thời điểm mà vật có vận tốc chỉ bằng 4π cm/s cho đến khi mà thời điểm vật đó có gia tốc bằng 1,6 m/s2 như sau:
- 1/6 s. B. 1/12 s. C. 1/24 s. D. 1/18 s.
Bài giải:
Xác định được khoảng thời gian, suy ra dùng đến đường tròn đa trục.
f = 2 Hzω = 4π rad/s
A = 2 cm
vmax = 8π cm/s
amax = 32 m/s2.
v = 4π cm/s tại điểm M, còn a = 1,6 m/s2 tại điểm N.
Từ điểm M đi đến điểm N có thể đi theo những cung sau đây: cung M1N1, cung M1N2, cung M2N1, cung M2N2.
Cung M1N1 thì ta sẽ có Δφmin = π : 6
Δtmin = 1 : 24 s.
Bài tập 3: cho vật nhỏ có dao động điều hòa nằm trên trục Ox, biên độ bằng 2 cm và tần số là 0,5 Hz. Lấy gần đúng với π2 = 10. Trong cùng một chu kì với khoảng thời gian vật có được loại vận tốc bé hơn √2cm/s, gia tốc sẽ lớn hơn 10 cm/s2 bằng
- 7/24 s. B. 5/12 s.
- 7/12 s. D. 5/24 s.
Bài giải:
ứng với cung lớn M1M2
a = 10 cm/s2 tại điểm N,
a > 10 cm/s2 ứng cung nhỏ N1N2
Cung nhỏ N2M1 không được tô đậm sẽ thỏa mãn đủ 2 điều kiện trên của v và a :
Δφ = 7π : 12 suy ra Δt = 7/12 s.