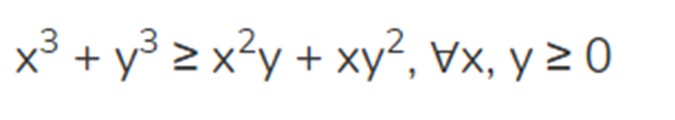Trong lĩnh việc giáo dục, học đường, toán học luôn là một trong những môn học khiến nhiều học sinh đau đầu, lo lắng và sợ hãi. Với nhiều công thức, hăng đẳng thức, định lý, định nghĩa… khác nhau từ toán hình học đến toán số học. Bài viết ngày hôm nay sẽ giúp các bạn học sinh phần nào giảm bớt được cảm giác sợ hãi trong việc đối mặt với môn học này. Thông qua việc hệ thống lại khái niệm, định nghĩa cũng như tính chất của bất đẳng thức. Bên cạnh đó, bài viết còn kèm theo một số ví dụ để các bạn hiểu rõ và dễ áp dụng hơn vào bài học. Nên hãy theo dõi bài viết đến cuối cùng các bạn nhé!

Khái niệm, định nghĩa của bất dẳng thức:
Định nghĩa
Bất đăng thức là một công thức toán học xuất hiện lần đầu trong chương trình học tập của học sinh Việt Nam là trong giáo trình sách giáo khoa lớp 8. Bắt đầu từ lúc đó, học sinh bắt đầu tiếp xúc với hàng loạt các dạng bất đẳng thức khác nhau. Cho đến năm lớp 10, các em sẽ tiếp tục làm quen với một loại bất đẳng thức mới, được gọi là bất đẳng thức Cauchy (hay bất đẳng thức Cô – Si). Bây giờ chúng ta đi từng bước tìm hiểu về các bất đăng thức này nhé.
Khái niệm của bất đẳng thức:
Một mệnh đề hay hệ thức có các dạng như sau:
- A > B
- A < B
- A ≥ B
- A ≤ B
Thì được gọi là bất đẳng thức.
Trong đó:
A, B là các biểu thức về các phép toán
A: thường được gọi là vế trái của bất đẳng thức;
B: ngược lại, được gọi là vế phải của bất đăng thức.
Mối quan hệ tương đương và hệ quả của một bất đẳng thức:
- C < D được gọi là bất đẳng thức hệ quả của bất đẳng thất A < B nếu mệnh đề “A < B → C < D“.
- Bất đẳng thức tương đương xảy ra trong trường hợp: A < B → A < D và C < D → A < B là mệnh đề đúng thì hai bất đẳng thức này (A < B và C < D) được gọi là bất đẳng thức tương đương. Và được kí hiệu là “A < B <=> C < D“
Tham khảo thêm về các công thức toán học khác :
- Tổng hợp công thức tính diện tích và chu vi hình chữ nhật
- Công thức tính chu vi và diện tích hình thoi chuẩn SGK
- Cách tính thể tích & diện tích hình chóp tứ giác đều chuẩn
- Công thức tính diện tích hình trụ, hình nón chuẩn
Tính chất của bất đẳng thức
Với định nghĩa trên của bất đăng thức thì ta có được một số các tính chất sau đây về bất đẳng thức:
Cộng hai vế của một bất đẳng thúc với cùng 1 số:
Tính chất này được hiểu như sau: khi ta cộng một số (cùng giá trị) vào hai vế của một bất đăng thức thì ta được một bất đăng thức mới với chiều cùng với bất đẳng thức cũ.
Ta có :
A < B thì cộng C là một số bất kì (cùng giá trị) A + C < B + C.
Nhân 2 vế của 1 bất đẳng thức cùng với 1 số:
Khi ta nhân hai vế của một bất đẳng thức cho một số bất kì, ta sẽ có 2 trường hợp sau đây:
- Trường hợp 1 :
Với C là số tự nhiên nhỏ hơn 0.
Khi đó:
A < B <=> A.C > B.C
- Trường hợp 2 :
Với C là một số tự nhiên lớn hơn 0.
Khi đó :
A < B <=> A.C < B.C
Cộng 2 bất đẳng thức cùng chiều :
Khi cộng 2 bất đẳng thức cùng chiều ta được một bất đẳng thức mới như sau:
Ta có :
A < B và C < D
A + C < B + D
Nhân 2 bất đẳng thức cũng chiều :
Khác với tính chất trên, tính chất nhân 2 bất đẳng thức cũng chiều này xảy ra khi đáp ứng được đủ 2 kiều điện sau:
Với A và C đều là 2 số tự nhiên lớn hơn 0.
Khi đó :
A < B và C < D
A.C < B.D
Nâng 2 vế của bất đẳng thứ lên thêm một lũy thừa:
Đối với tính chất này của bất đẳng thức, ta lưu ý, có đến 2 trường hợp xảy ra.
- Trường hợp 1:
Với n N*, khi đó:
A < B <=> A2n + 1 < B2n + 1
- Trường hợp 2:
Với n ∈ N* và A > 0, khi đó:
A < B <=> A2n < B2n
Khai căn 2 vế của một bất đẳng thứ:
Cũng nhứ tính chất nâng thêm một bật lũy thừa phía trên. Tính chất này của bất đẳng thức cũng xảy ra 2 tường hợp khác nhau.
- Trường hợp 1:
Với A > 0 thì:
A < B <=> A < B
- Trường hợp 2:
Với A là một số bất kỳ, tùy ý (có thể lớn hơn 0 hoặc nhỏ hơn 0), lúc đó:
A < B <=> 3A < 3B
Tính chất bắt cầu của bất đẳng thức:
Đây được xem như là tính chất cơ bản nhất của hệ thống các bất đẳng thức.
Nếu ta có:
A < B và B < C
<=> A < C
Bất đẳng thức Cauchy (bất đẳng thức Cosi)
Đây được coi như là một dạng bất đẳng thức giữa trung bình nhân và trung bình cộng của biểu thức.
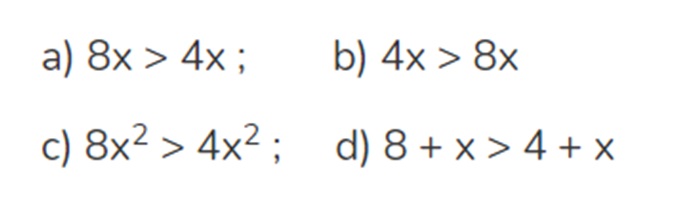
Ta có công thức tính trung bình cộng của 2 số như sau = A + B2
Khi đó, công thức tính trung bình cộng của n số được phát biểu là = A1 + A2 + … + Ann
Trung bình nhân của hai số không âm (A 0 và B 0) = AB
Từ đó, ta có công thức trung bình nhân của n số không âm (A1, A2, … An 0) như sau nA1. A2. … .An
Định lý bất đẳng thức Cauchy với 2 số không âm:
Từ các yếu tố trên, ta có thể phát biểu định lý bất đẳng thức Cauchy như sau:
A + B2 = AB (với A 0 và B 0).
Dấu “=” chỉ xảy ra khi và chỉ khi A = B.
Định lý bất đẳng thức Cauchy mở rộng:
Từ đính lý bất đẳng thức gốc của Cauchy ta vừa định nghĩa, ta có thể phát triển thêm bất đẳng thức mở rộng của nó và được phát biểu như sau:
A + B + C2 = ABC (với A 0, B 0 và C 0).
A1 + A2 + … + Ann = nA1. A2. … .An (với A1, A2, … An 0).
Một số ví dụ, áp dụng về bất đẳng thức:
Bài tập 1:
Trong các bất đẳng thức sau, hãy xác định bất đẳng thức nào luôn đúng (với mọi giá trị của x)
Bất đẳng thức nào đúng với mọi giá trị của x?
Lời giải:
Đáp án đúng là câu d với bất đẳng thức: 8 + x > 4 + x
Vì 8 luôn luôn lớn hơn 4 nên áp dụng tính chất cộng 2 vế của một bất đẳng thức với 1 số tự nhiên bất kỳ ta có được 8 + x > 4 + x
Vì sao các đáp án kia sai?
Câu a : 8x > 4x
Điều này đúng khi và chỉ khi x là một số lớn hơn 0 chứ hông đúng trong mọi giá trị của x
Câu b : 4x > 8x
Trái ngược với đáp án a ở trên thì bất đẳng thức này chỉ đúng khi x là một số âm (tức x là 1 số bé hơn) và vẫn không đúng trong mọi giá trị của x.
Câu c : 8x2 > 4x2
Tương tự như 2 đáp án a và c trên. Bất đẳng thức này cũng chỉ đúng trong trường hợp nhất định: khi và chỉ khi x ≠ 0, không đáp ứng được yêu cầu với mọi giá trị của x của đề bài.
Bài tập 2:
Chứng minh bất đẳng thức trên (với x và y 0) là đúng
Ta có:
x và y 0 x + y 0
(Áp dụng các tính chất của bất đẳng thức)
x3 + y3 x2y + xy2
<=> (x3 + y3) – (x2y + xy2) 0
<=> (x + y)( x2 – xy + y2) – xy(x + y) 0
<=> (x + y)( x2 – xy + y2 – xy) 0
<=> (x + y)( x2 – 2xy + y2) 0
<=> (x + y)(x – y)2 0 (luôn đúng vì x + y và (x – y)2 0)
Dấu “=” chỉ xảy ra khi và chỉ khi (x – y)2 0 <=> x = y