Hình vuông, hình chữ nhật, hình tròn, hình tam giác là các hình học cơ bản mà chúng ta đã được tiếp cận khi còn rất bé thông qua những bài hát, trò chơi mấu giáo, tiểu học. Hệ thống các công thức tính chu vi, diện tích, thể tích là các công thức cơ bản ở cấp tiểu học. Bài viết sau đây sẽ giúp bạn đọc ôn lại những kiến thức cơ bản của toán học. Chúng ta sẽ bắt đầu với tính diện tích hình vuông và các công thức của nó: công thức tính chu vi hình vuông, công thức tính thể tích hình vuông thì chúng ta theo dõi dưới đây nhé.
Khái niệm hình vuông là gì?
Trước khi đi vào tìm hiểu các công thức tính diện tích hình vuông, chu vi hình vuông và thể tích hình vuông ta làm quen với một số khái niệm, đặc điểm và dấu hiệu nhận biết về hình vuông trước.
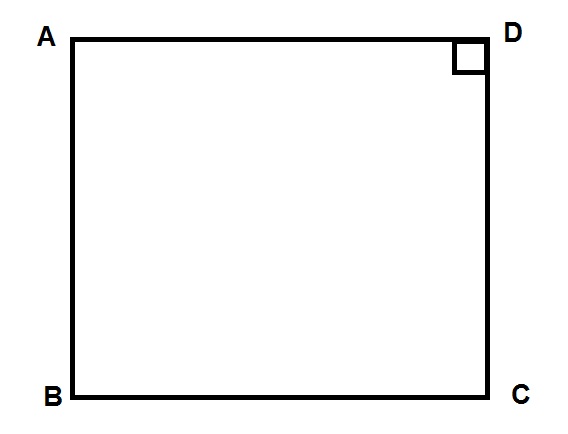
Hình vuông là một tứ giác có 4 cạnh bằng nhau, có 4 góc vuông hay hình vuông còn được gọi là hình tứ giác đều.
Tiếp đến, chúng ta cùng điểm sơ qua các đặc điểm của hình vuông trước khi tìm hiểu về công thức tính chu vu, công thức tính thể tích, tính diện tích hình vuông.
Tham khảo thêm các cách tính diện tích hình học khác :
- Công thức tính chu vi và diện tích hình thoi chuẩn SGK
- Công thức tính diện tích hình bình hành, chu vi kèm 5 ví dụ
- Cách tính thể tích & diện tích hình chóp tứ giác đều chuẩn
- Tổng hợp công thức tính diện tích và chu vi hình chữ nhật
Đặc điểm, tính chất của hình vuông:
Như chúng ta biết thì chu vi hình vuông diện tích hình vuông cũng cần phải dựa vào một số các khái niệm và tính chất của hình vuông mới đưa ra được công thức chuẩn . Cụ thể chúng ta tìm hiểu rõ hơn về hình vuông.
Đặc điểm của hình vuông:
- Hình chữ nhật nếu có các cạnh (4 cạnh) bằng nhau là hình vuông.
- Hình thoi nếu có 2 đường chéo nhau thì là hình vuông.
- Hình vuông vừa là hình thoi vừa là hình chữ nhật.
Xác định đặc điểm của hình vuông rồi mới bắt đầu áp dụng công thức tính chu vi và diện tích hình vuông cho phù hợp.
Hình vuông có các tính chất sau đây:
- Trong hình vuông, hai đường chéo vuông góc và bằng nhau, và chúng giao nhau tại trung điểm (điểm chính giữa) của mỗi đường.
- Tâm của đường tròn ngoại tiếp và nội tiếp của hình vuông chính là giao điểm của hai đường chéo trong hình vuông.
- Giao điểm của các đường phân giác, trung tuyến, trung trực trong hình vuông đều trùng nhau tại một điểm.
- Hình vuông sẽ được chia thành hai nữa bằng nhau khi có một đường chéo đi qua 2 điểm đối diện của hình vuông.
- Trong hình vuông, giao điểm của hai đường chéo của hình vuông trùng nhau tại trung điểm của mỗi đường, đồng thời cũng là tâm của cả hai đường tròn nội tiệp và ngoại tiếp hình vuông.
- Tất cả các tính chất của hình chữ nhật cũng như hình thoi đều có trong tính chất của một hình vuông.
Các cạnh đều vuông góc
Tiếp đến ta cùng tìm hiểu về các dấu hiện nhận biết của hình vuông, để xác định đúng hình từ đó áp dụng các công thức tính toán: công thức tính thể thích hình vuông , công thức tính chu vi hình vuông và diện tích hình vuông.
Các dấu hiệu nhận biết hình vuông là gì?
- Nếu một hình chữ nhật có độ dài hai cạnh kề bằng nhau → là hình vuông.
- Nếu hai đường chéo của một hình chữ nhật vuông góc với nhau tại trung điểm của mỗi đường → là hình vuông.
- Trong một hình chữ nhật nếu đường phân giác 1 góc trùng với đường chéo của hình chữ nhật → là hình chữ nhật.
- Nếu hình thoi có một góc vuông → là hình vuông.
- Nếu đường chéo của một hình thoi bằng nhau → là hình vuông.
Sau khi tìm hiểu hết một lượt về khái niệm, các đặc điểm, tính chất cũng như dấu hiệu nhận biết của hình vuông. Từ đó, ta có đủ cơ sở để cùng đi tìm hiểu hệ thống các công thức tính toán về hình vuông. Ta sẽ cũng tìm hiểu, ôn lại 3 công thức chính của hình vuông: công thức tính thể tích, công thức tính chu vi hình vuông, diện tích hình vuông.
Công thức tính chu vi hình vuông:
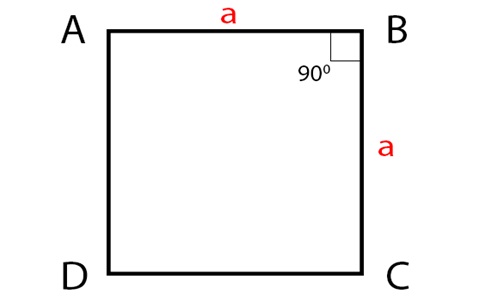
Xét một hình vuông ABCD, có độ dài cạnh là a:Chu vi hình vuông được xác định bằng tổng độ dài bốn cạnh của hình vuông. Từ đó, ta có công thức chu vi hình vuông là:
P = a + a + a + a = a x 4
Nửa chu vi hình vuông được xác định bằng tổng độ dài 2 cạnh của hình vuông hoặc 12 chu vi của hình vuông. Từ đó, ta có công thức nữa chu vi hình vuông là:
Nửa chu vi hình vuông = a + a = a x 2 = 12 P
Tiếp theo sẽ đến công thức tính diện tích hình vuông. Mời các bạn cùng theo dõi tiếp bài viết.
Công thức tính diện tích hình vuông:
Xét một hình vuông ABCD, có độ dài cạnh là a. Diện tích hình vuông được xác định bằng tích độ dài 2 cạnh kề nhau của hình vuông. Từ đó, ta có công thức tính diện tích hình vuông như sau:
S = a x a = a2
Công thức tính thể tích hình lập phương:
Từ công thức diện tích hình hộp chúng ta có công thức tính thể tích. Khi tính thể tích của một hình vuông, chính là nói đến tính thể tích của một khối lập phương ( khối lập phương là một hình khối 3 chiều, có 2 mặt đáy song song và 4 mặt xung quanh đều là hình vuông ).
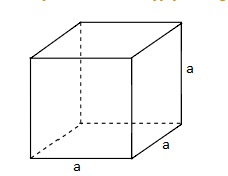
Thể tích của hình lập phương được xác định bằng tích của diện tích mặt đáy và chiều cao (a) của hình lập phương đó. Từ đó, ta có công thức tính thể tích hình vuông (thể tích hình lập phương) như sau:
V = S x a
Với tính chất hình chữ nhật các cạnh đều cùng nhau nên ta có công thức tính thể tích đơn giản hơn
V = a x a x a = a3
Một số ví dụ về công thức diện tích hình vuông:
Với tổng hợp các bài tập về chu vi, diện tích và thể tích hình vuông ở trên thì Legoland đã tổng hợp được những bài tập giúp các bạn học sinh có thêm những luyện tập tố hơn trong các công thức tính diện tích và chu vi đối với các vật thể hình vuông tốt nhất và nhớ lâu hơn . Dưới đây là tuyển tập các ví dụ cụ thể về chu vi và diện tích nhé.
Bài tập 1 (bài toán thuận):
Cho một miếng đất hình vuông có chiều dài cạnh là 50 mm, hãy xác định công thức tính chu vi hình vuông, diện tích hình vuông của tấm vải là bao nhiêu cm, cm2?
Đổi 50 mm = 5 cm
(Dựa vào công tính chu vi hình vuông và diện tích hình vuông ở trên)
Chu vi tấm vải là:
- P = 5 + 5 + 5 + 5 = 5 x 4 = 20 (cm)
Diện tích tấm vải là:
- S = 5 x 5 = 52 = 25 (cm2)
Bài tập 2 (bài toán ngược):
Cho một viên gạch hình vuông có nửa chu vi là 6 cm. Hãy tìm độ dài cạnh, diện tích và thể tích của viên gạch đó?
Gọi a là chiều dài cạnh của viên gạch
( Dựa vào công thức tính chu vi hình vuông, công thức tính thể tích hình vuông và công thức tính diện tích hình vuông ở trên)
Độ dài cạnh của viên gạch là:
- 12 P = 6 → 2 x a = 6 → a = 6 : 2 → a = 3 (cm)
Diện tích hình vuông của viên gạch là:
- S = 3 x 3 = 32 = 9 (cm2)
Thể tích của viên gạch là:
- V = 3 x 3 x 3 =33 = 21 (cm3)
Ứng dụng của diện tích, chu vi và thể tích hình vuông trong thực tiễn:
Chúng ta có thể dễ dàng bắt gặp các vật dụng hằng ngày, dễ quan sát nhất là những vật dụng tại nhà, trường học hay nơi làm việc, không khó gì để tìm kiếm một vật dụng có hình vuông như: viện gạch, cục gôm, chiếc gương cầm tay, tủ đầu giường, mặt ghế, cửa sổ,… đặc biệt phải kể đến một loại bánh truyền thống được lưu lại trong lịch sử nước Việt Nam ta, chính là bánh chưng. Ta có thể thấy các ứng dụng của hình vuông là rất nhiều trong đòi sống của chúng ta.

Bên cạnh đó, các hệ thống công thức tính chu vi hình vuông, diện tích, thể tích hình vuông đều có tính ứng dụng rất cao. Ví dụ như trong xây dưng, công thức tính chu vi, diện tích hình vuông giúp ta tính toán được cần bao nhiêu viên gạch đê lát đủ một nền nhà hoặc ta có thể sử dụng công thức tính thể tích để tính xem một hồ nước, bể bơi hình vuông cần đổ bao nhiêu lít để lắp đầy,…
Qua đó, ta có thể thấy công thức tính chu vi hình vuông, công thức tính thể tích hình vuông và diện tích hình vuông nói riêng và các công thức tính toán toán học nói riêng đều có những áp dụng rất hữu ích vào thực tiễn, giúp con người làm việc hiệu quả, năng suất hơn. Vì thế, các công thức toán học không phải vô ích và khô khan như chúng ta thường hay nghĩ mà nó rất có ích trong đời sống của con người đây nhé! Nên hãy tìm hiểu, học tập và ôn tập các công thức toán học thật chăm chỉ nhé!