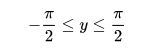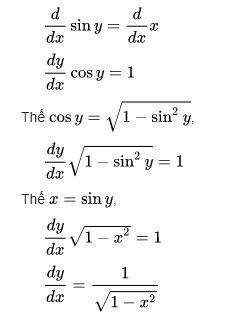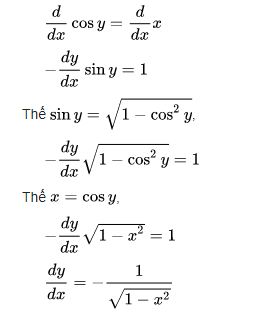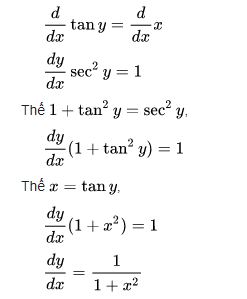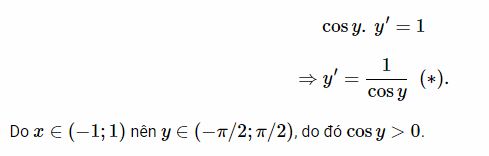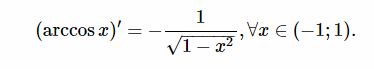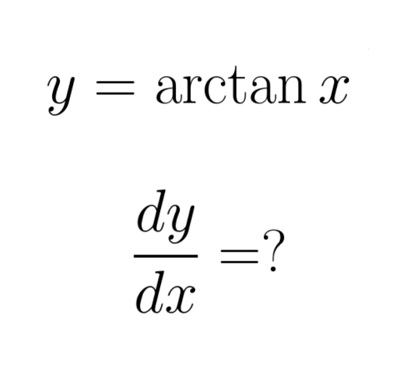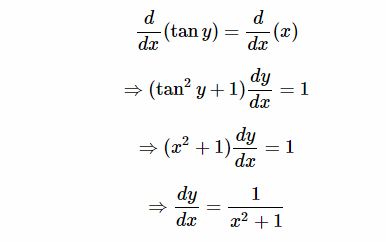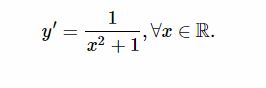Các công thức đạo hàm arctan, arcsin, arccos kèm 5 ví dụ hay

Trong toán học có khá nhiều công thức khác nhau , đặc biệt trong các công thức đạo hàm lượng giác thì đạo hàm Arctan, arcsin, arccos là một trong những hàm được sử dụng khá phổ biến trong chương trình trình học cấp 2 cấp 3 . Ngoài ra công thức đạo hàm Arctan cũng xuất hiện rất nhiều ở trong các chương trình thi hết học kỳ , thi tốt nghiệp và thi đại học .

Arctan là gì?

Arctan là một hàm số ngược trong công thức đạo hàm lượng giác trong toán học . Hay nói cách khác là căn thức của hàm số tan

Các điều kiện để tồn tại hàm số ngược :

Các công thức đạo hàm Arctang , Arccos, Arcsin

Tham khảo thêm :

Công thức đạo hàm Arcsin

Cho

$y = arcsin x$

Trong đó :

Thì ta có : sin y = x

Dùng đạo hàm ẩn và giải dy/dx:

Công thức đạo hàm Arccos

Cho hàm số : y = Arccos x

trong đó

$0 \le y \le \pi$

Thì ta có : Cos y = x

Dùng đạo hàm ẩn và giải dy/dx:

Công thức đạo hàm Arctang

Cho hàm số : y = Arctang x

Trong đó :

Thì ta có :

tan y = x

Dùng đạo hàm ẩn và giải dy/dx ta được :

Công thức đạo hàm lượng giác ngược

(Hàm lượng giác ngược có 2 cách viết, ví dụ hàm số lượng giác ngược của $\sin(x)$ có thể viết thành là $sin^{-1}(x)$ hoặc $\arcsin(x)$ , mình chọn cách viết thứ hai.)

Đạo hàm của $\arcsin$ : $y = \arcsin(x) \Rightarrow y' = \frac{1}{\sqrt{1 - x^2}}$

Đạo hàm của $\arccos$ : $y = \arccos(x) \Rightarrow y' = -\frac{1}{\sqrt{1 - x^2}}$

Đạo hàm của $\arctan$ : $y = \arctan(x) \Rightarrow y' = \frac{1}{1 + x^2}$

Đạo hàm của $\text{arccot}$ : $y = \text{arccot}(x) \Rightarrow y' = -\frac{1}{1 + x^2}$

Đạo hàm của $\text{arcsec}$ : $y = \text{arcsec}(x) \Rightarrow y' = \frac{1}{|x| \sqrt{x^2 - 1}}$

Đạo hàm của $\text{arccsc}$ : $y = \text{arccsc}(x) \Rightarrow y' = -\frac{1}{|x| \sqrt{x^2 - 1}}$

Tổng hợp các bài tập liên quan đến các đạo hàm arctan hay nhất

Bài 1 : Tính đạo hàm của hàm số y=arcsinx trên khoảng (−1;1).

Lơi giải :

Theo định nghĩa hàm lượng giác ngược, từ y=arcsinx ta có:

sin y = x .

Lấy đạo hàm theo biến x hai vế ta được:

Bài 2 : Tính đạo hàm của hàm số y=arccosx trên khoảng (−1;1).

Lời giải :

Tương tự như lời giải bài toán 1 với lưu ý arccos x=y∈(0;π), ta được:

Bài 3 : Tính đạo hàm của hàm số y=arctan x

Lời giải :

Từ y=arctan x và định nghĩa hàm arctan ta có : tan y = x. Chúng ta sẽ lấy đạo hàm theo biến x ta được:

Vậy đạo hàm của hàm số y= arctan x là:

Tổng kết :

Đó chính là tổng hợp các kiến thức về công thức đạo hàm arctan , đạo hàm Arcsin và đạo hàm arccos được Legoland tổng hợp kèm theo các ví dụ cụ thể để giúp các bạn thực hành luôn và nhớ lâu hơn nhé .